L'OULIPO, entre maths et poésie
Comment peut-on compléter deux domaines totalement différents pour créer quelque chose de nouveau ?
L’Oulipo est un organisme artistique réunissant mathématiciens et littéraires. Fondée en 1960, cette organisation se réunit autour de l’écrivain Raymond Queneau et du mathématicien François Le Lionnais. L’Oulipo est un acronyme désignant l’Ouvroir de Littérature Potentielle : les participants se réunissent en un lieu isolé pour innover et inventer de nouvelles techniques, sans savoir si l’effort sera récompensé. La volonté propre à ce groupe est d’écrire en s’inspirant de la rigueur mathématique et du jeu.
Les membres se fixent des règles à suivre qui les poussent à reconstruire leur manière d’écrire et font surgir la littérature potentielle de leur plume. Ils utilisent souvent des techniques mathématiques pour créer des poèmes. À première vue, cela semble totalement insensé, impossible à mettre en pratique. Comment utiliser les maths dans la littérature ?
Ces règles se construisent autour de plusieurs tendances, comme rechercher de nouvelles structures définies par des contraintes pouvant être alphabétiques, numériques et phonétiques. Dans « 41 sonnets irrationnels », Jacques Bens construits autour de la contrainte numérique, utilisant les quatre premiers chiffres de π en nombre de vers par strophes. Créer sinon de nouveaux textes à partir d’œuvres existantes. Le meilleur exemple de cette « littérature combinatoire » est l’ouvrage de Raymond Queneau, l’un des fondateurs de l’Oulipo : Cent mille milliards de poèmes (1961).
À partir d’un poème existant de 10 sonnets (poèmes de 14 vers en alexandrins, organisé en 2 quatrains et 2 tercets), la contrainte permet de créer de nouveaux poèmes : on prend un vers du premier sonnet, suivis d’un vers du deuxième, et ainsi de suite. Il faut bien sûr que les rimes et structures syntaxiques soient compatibles entre elles. Nous avons alors 10 choix pour le premier poème, suivi de 10 choix pour le deuxième, etc., pouvant former un total de 1014 choix, soit 100 000 000 000 000 poèmes. La poésie est donc combinatoire.
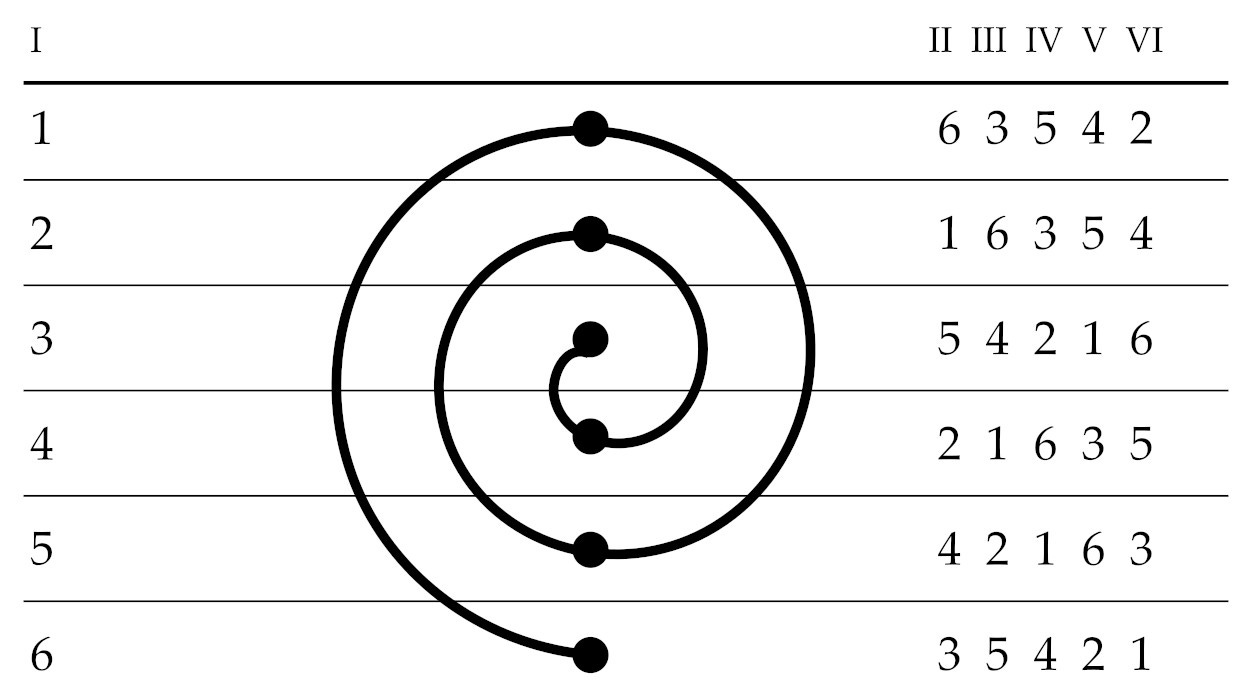
Autre exemple, à partir de la forme de la sextine (poème de 6 strophes de 6 vers chacun et d’une demi-strophe de 3 vers, l’Oulipo a développé la quenine, ou n-ine. Toutes les strophes possèdent les mêmes mots à la rime, mais ils sont échangés suivant une permutation en spirale (comme sur le schéma). Si on numérote ces rimes 123456 (pour 6 vers), nous avons donc, en les lisant dans l’ordre sur la spirale : 123456, 615243, 364125, 532614, 451362 et 246531. Les quenines généralisent la sextine en n strophes de n vers, avec les permutations (1, 2, 3, .., n) qui deviennent (n-1, n-1, 2, n-2, n-3, ...). Les quenines ne sont valables que pour certains nombres : pour d’autres, les permutations reviennent à l’état initial avant d’arriver au n-nombre de strophes. Cette suite de nombre est aussi appelée suite fondamentale de Queneau.
L’Oulipo ne se limite pas dans son utilisation mathématique. On retrouve par exemple des livres comme La Disparition de Georges Perec, qui est écrit entièrement sans la lettre [e]. Comme dit précédemment, L’Oulipo est une écriture avec contrainte pour permettre de développer sa créativité en ayant des idées saugrenues : les mathématiques ne sont qu’un outil pour arriver à cette fin.
« Ce n’est pas un mouvement littéraire.
Ce n’est pas un séminaire scientifique.
Ce n’est pas de la littérature aléatoire
Ses recherches sont naïves, artisanales et amusantes. »- Raymond Queneau, Bâtons, chiffres et lettres (1994)
Les cartouches
Tony :
L’utilisation d’objets mathématiques pour créer de nouvelles formes de poèmes ou de nouveaux styles d’écriture est intéressante, mais reste tout de même superficielle. L’Oulipo semble plus être un jeu, plutôt qu’une véritable et nouvelle forme d’art.
Dji :
Une découverte qui changera sans doute ma vision de l’écriture. L’utilisation des contraintes dans l’écriture existait déjà dans mon univers, mais je n’avais jamais lié les mathématiques à cette notion. Impressionné par ce qu’ils ont réussi à créer, j’espère avoir le temps d’essayer ces nouvelles méthodes dans l’année à venir.
Sources :
« Cinq choses à savoir sur l’OuLiPo, le groupe littéraire mis en lumière par le Goncourt 2020 », Franceinfo, 30 nov. 2020 [en ligne]. Disponible sur : francetvinfo.fr/culture/livres/cinq-choses-a-savoir-sur-l-oulipo-le-mouvement-litteraire-mis-en-lumiere-par-le-goncourt-2020_4201577.html
« N-ine », Oulipo, 25 juin 2007 [en ligne]. Disponible sur : oulipo.net/fr/contraintes/n-ine
AUDIN M. « L’Oulipo et les mathématiques. Une description ». Conférence à la médiathèque les Champs libres de Rennes, 20 oct. 2010 [en ligne]. Disponible sur : docplayer.fr/2941482-L-oulipo-et-les-mathematiques-une-description-par-michele-audin.html
AUDIN M., MONK I. et JOUET J. « OuLiPo : contraintes mathématiques et création littéraire », Institut Français de la Mode, 29 juin 2019 [en ligne]. Disponible sur : ifmparis.fr/fr/podcasts/ou-li-po-contraintes-mathematiques-et-creation-litteraire
Nicolas. « 1, 2, 3, 5, 6, 9... et après ? », Desmaths, 24 oct. 2021 [en ligne]. Disponible sur : des-maths.fr/2021/10/24/1-2-3-5-6-9-et-apres
Zalmanski A. « L’OuLiPo, une écriture mathématique », Pour la Science, 1 avr. 2005 [en ligne]. Disponible sur : pourlascience.fr/sd/histoire-sciences/l-oulipo-une-ecriture-mathematique-5720.php





